Path search

Here, PathMap is used to find paths to all other points on a grid around an attachment site. Grid points (voxels) that are occupied by the structure are obstacles in the path search.

import pylab as plt
import pathlib

import IMP
import IMP.core
import IMP.atom
import IMP.bff
import IMP.em

Setup of system

In this example we search the path from a single attachment site of a label to all other points in space within the reach of the label. First, we create a new IMP model and load the coordinates from a PDB file. The atoms in the PDB file will serve as obstacles the coordinates of an atom of the corresponding structure will be the starting point for the path search.

m = IMP.Model()
pdb_fn = pathlib.Path(IMP.bff.get_example_path('structure')) / "T4L/3GUN.pdb"
hier = IMP.atom.read_pdb(str(pdb_fn), m)

sel = IMP.atom.Selection(hier)
sel.set_chain_id('A')
sel.set_residue_index(132)
sel.set_atom_type(IMP.atom.AtomType('CB'))
sel_particles = sel.get_selected_particles()
labeled_p = IMP.core.XYZ(sel_particles[0])
path_origin = labeled_p.get_coordinates()

Initializing a PathMap

Next, we create a header for the PathMap. The PathMap header contains information on the maximum path-length, the grid spacing, the ‘neighbor radius’ (a parameter that is used to define the neighboring grid points), and an obstacle threshold. The maximal path length parameter determines the size of the grid and the grid spacing determines the resolution of the grid. In a first step the density of obstacles on the grid is samples. The obstacle threshold parameter defines what density is used to define a grid point as occupied. Grid points (voxels) are connected by edges. The neighbor_radius parameter defines how far apart voxels can be separated and still be considered as connected. With a PathMapHeader a new PathMap can be created.

path_map_header_parameter = {
    "max_path_length": 20.0,
    "grid_spacing": 1.0,
    "neighbor_radius": 2,
    "obstacle_threshold": 1e-5
}
path_map_header = IMP.bff.PathMapHeader(**path_map_header_parameter)
path_map_header.set_path_origin(path_origin)
path_map = IMP.bff.PathMap(path_map_header)

Setup of obstacles

IMP particles (with XYZR decorator) can be used to define obstacles in a PathMap. The obstacles can be sampled with an additional (extra radius). Each voxel in a PathMap has an associated tile, that is connected via edges to other tiles of the map. Tiles that are on places of obstacles do not have edges. After sampling the tiles and corresponding edges are updated.

ps = [a.get_particle() for a in IMP.atom.get_leaves(hier)]
path_map.set_particles(ps)
path_map.sample_obstacles(extra_radius=0.0)
# The origin is located on an atom and hence blocked. Thus, there cannot be
# a path to the origin. Hence, unblock sphere around the origin.
path_map.fill_sphere(path_origin, radius=3.0, value=0.0, inverse=False)
path_map.update_tiles()

The obstacles in a PathMap can be written to density files using standard IMP routines.

# IMP.em.write_map(path_map, "OBSTACLES.mrc")

Path search

The path search starts from a tile in the PathMap. Here, we start the path search at the origin (the center) of the PathMap. To find the distance from the start index to all other tiles we use the Dijkstra algorithm and search for an index not in the PathMap (default: -1)

start_idx = path_map.get_voxel_by_location(path_origin)
path_map.find_path_dijkstra(start_idx, -1)  # if the end_idx

Now, we can backtrace the shortest path from every tile (voxel) to the start index. A path is a sequence of tile/voxel ids.

t = path_map.get_tiles()
end_idx_1 = 829
path_1 = t[end_idx_1].backtrack_to_path()
print(path_1)

end_idx_2 = 229
path_2 = t[end_idx_2].backtrack_to_path()
print(path_2)

(32820, 31180, 29540, 27900, 24700, 21500, 18300, 16701, 15102, 13503, 10303, 8704, 7105, 5506, 3947, 2388, 829)
(32820, 31180, 29540, 27901, 26301, 24662, 23023, 21383, 19743, 18103, 16463, 13263, 11624, 9985, 8346, 6707, 5068, 3429, 229)

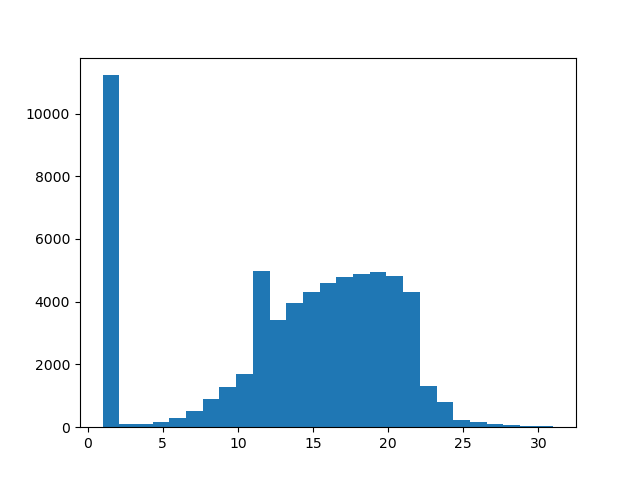
Not to all tiles a path can be found. A tile without a path to the starting tile has a path-length of 1.

paths = [t[e].backtrack_to_path() for e in range(path_map.get_number_of_voxels())]
path_length = [len(p) for p in paths]
plt.hist(path_length, 27)
plt.show()

no_paths = [i for i, p in enumerate(paths) if len(p) <= 1]

Tile feature

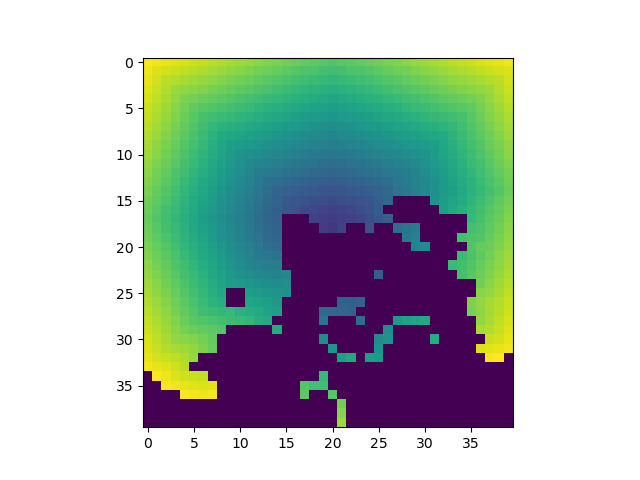
The most important attributes of tiles are the penalty and the cost of visiting a tile (from the starting point). Additionally, a tile has a density, e.g., used to implement weighted accessible volumes and a set of other (user-defined) features that are stored in a dictionary.

bounds = 0.0, 30
BFF_TILE_PENALTY = path_map.get_tile_values(IMP.bff.PM_TILE_PENALTY, (0, 1))
PM_TILE_COST = path_map.get_tile_values(IMP.bff.PM_TILE_COST, bounds)
PM_TILE_COST_DENSITY = path_map.get_tile_values(IMP.bff.PM_TILE_COST_DENSITY, bounds)

These features are returned as 3D arrays.

plt.imshow(PM_TILE_COST_DENSITY[16])
plt.show()

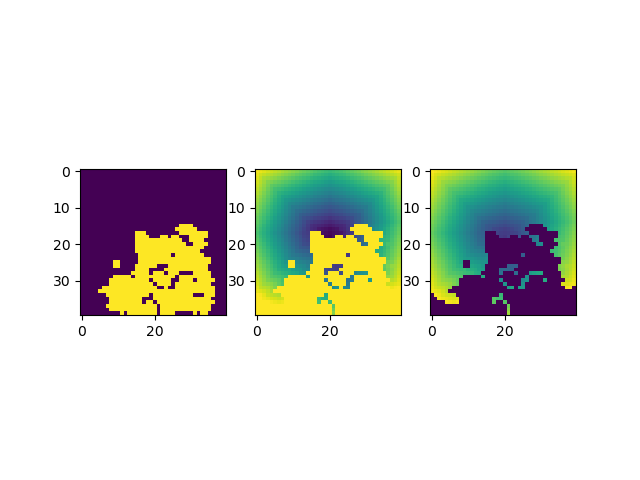
These features are returned as three dimensional arrays.

fig, axs = plt.subplots(1, 3, sharex=True)
axs[0].imshow(BFF_TILE_PENALTY[16])
axs[1].imshow(PM_TILE_COST[16])
axs[2].imshow(PM_TILE_COST_DENSITY[16])
plt.show()