Path searches

IMP.bff can to search for an optimal path on a grid with obstacles between two points using established algorithms (e.g., Dijkstra and A star). These path search algorithms can be used to implement accessible volume calculations of label for fluorescence or EPR experiments in a 1:N (one starting node N end nodes) path search (Dijkstra) or for 1:1 (one start node one end node) path searches (Astar), e.g., for implementing cross-linking restraints.

import pylab as plt
import pathlib
import numpy as np

import IMP
import IMP.core
import IMP.algebra
import IMP.atom
import IMP.bff
import IMP.em

Setup system

First, we create an IMP Model and a hierarchy from a PDB file. We select a residue in the hierarchy as a starting point for the path search. The starting point of the path search will be the central point of a 3D grid.

m = IMP.Model()
pdb_fn = pathlib.Path(IMP.bff.get_example_path('structure')) / "T4L/3GUN.pdb"
hier = IMP.atom.read_pdb(str(pdb_fn), m)

sel = IMP.atom.Selection(hier)
sel.set_chain_id('A')
sel.set_residue_index(132)
sel.set_atom_type(IMP.atom.AtomType('CB'))
sel_particles = sel.get_selected_particles()
labeled_p = IMP.core.XYZ(sel_particles[0])
path_origin = labeled_p.get_coordinates()

Create PathMapHeader

The PathMapHeader defines the grid spacing and the size of the grid used in the path search. The grid will have an edge that has twice the maximum path length.

path_map_header_parameter = {
    "max_path_length": 20.0,
    "grid_spacing": 1.0,
    "neighbor_radius": 2,
    "obstacle_threshold": 1e-5
}
path_map_header = IMP.bff.PathMapHeader(**path_map_header_parameter)
path_map_header.set_path_origin(path_origin)

Create PathMap, sample obstacles

After creating a PathMap assign particles to the map and sample the obstacles (assign densities to the grid).

path_map = IMP.bff.PathMap(path_map_header)
ps = [a.get_particle() for a in IMP.atom.get_leaves(hier)]
path_map.set_particles(ps)
path_map.sample_obstacles(extra_radius=0.0)

Get start/stop index

A path is searched from a start to an end point on the grid of the path map. The start and the end point are identified by their index. a points on the grid can be found by their cartesian coordinates.

start_idx = path_map.get_voxel_by_location(path_origin)
end_idx = 8062
r_end = path_map.get_location_by_voxel(end_idx)
r_start = path_map.get_location_by_voxel(start_idx)

Update tiles

Points on the grid are associated to tiles that have edges that connect to other (neighboring) tiles. Tiles that are occupied are not considered as neighbors and do not have edges connecting to them. After sampling obstacles tiles and edges of tiles should be updated. Updating the tiles resets the costs of visiting a tile. the cost of visiting a tile are updated by the path search (here Djikstra).

path_map.find_path_dijkstra(start_idx, end_idx)

Path-backtracking

After searching for a path, each tile has a predecessor (i.e., a tile that was the previous tile in a path search). Tile that have no predecessor were not visited. The predecessors are used to back track path from specific tile to start of the path search. We compare two path found by Djikstra and A-Star.

tiles = path_map.get_tiles()
path_dijkstra = tiles[end_idx].backtrack_to_path()

path_map.find_path_astar(start_idx, end_idx)
path_astar = path_map.get_tiles()[end_idx].backtrack_to_path()

Compare paths

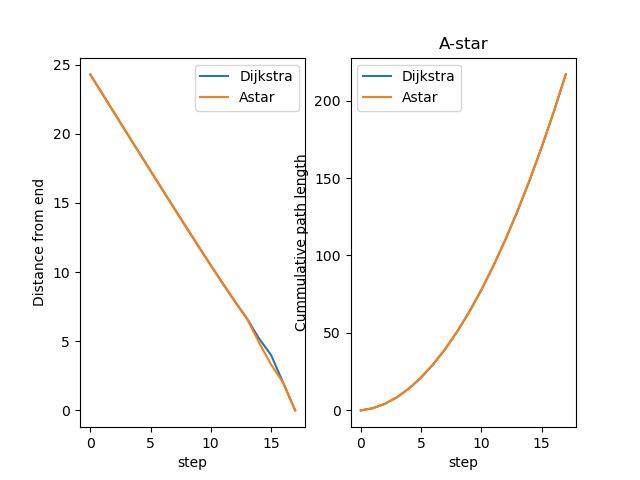
The A star algorithm uses the Eucledian distance to the end point as a heuristic in the search. While Djikstra solves the 1:N problem, i.e., searches for path from all points to the starting point. Thus, A-star and Djikstra find different path and A star is usually faster.

def get_distances(path):
    locations = [path_map.get_location_by_voxel(i) for i in path]
    distances_start = [IMP.algebra.get_distance(r_start, l) for l in locations]
    distances_end = [IMP.algebra.get_distance(r_end, l) for l in locations]
    return distances_start, distances_end

dsd, ded = get_distances(path_dijkstra)
dsa, dea = get_distances(path_astar)
fig, axs = plt.subplots(1, 2, sharex=True)
axs[0].set(xlabel='step', ylabel='Distance from end')
axs[0].plot(ded, label="Dijkstra")
axs[0].plot(dea, label="Astar")
axs[1].set(xlabel='step', ylabel='Cummulative path length')
axs[1].plot(np.cumsum(dsd), label="Dijkstra")
axs[1].plot(np.cumsum(dsa), label="Astar")
axs[1].set_title('A-star')
axs[0].legend()
axs[1].legend()
plt.show()